Types of Uncertainty: Overview (DRAFT)

The UQ Cycle: A General Framework for Uncertainty

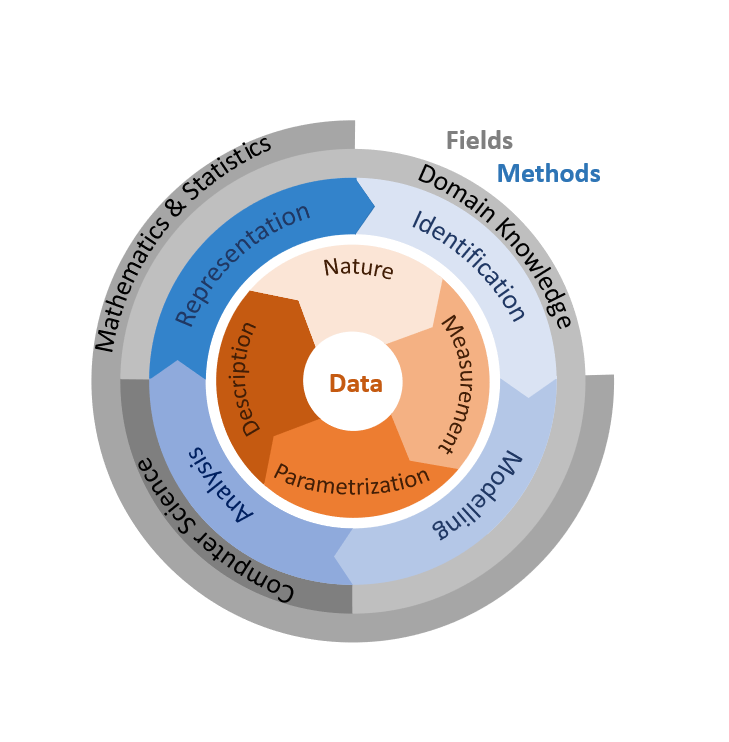
Fig. 4 The UQ Dictionary cycle summarizes dimensions of uncertainty with respect to its sources, domains and implication.

Different systems can be subject to epistemic, aleatoric, and ontological uncertainties. Epistemic uncertainty arises from a lack of knowledge about the system or phenomenon of interest. Epistemic uncertainty can also be referred to as information ambiguity, ignorance, reducible uncertainty, or subjective uncertainty. Aleatoric uncertainty arises due to the random nature in the process. Therefore, it can also be referred to as inherent random or stochastic uncertainty and in some systems it is known as physical variability. Using inappropriate methodology or belief systems results in ontological uncertainty. Data, models, or methodologies can be affected by ontological uncertainty which is unrecognized and unquantifiable.

In the current project, we are using the UQ cycle in which we group the uncertainty based on where it arises in the scientific process. This approach leads to the following data-induced types of uncertainties

Nautural Uncertainty: We typically approach nature with an interest in a particular process and conceptual framework for understanding it. This shapes which aspect of nature we measure and why. But natural processes are often stochastic to some degree. This stochasticity can arise due to the effect of phenomena that in principle could be measured but in practicality cannot be. Thus, natural uncertainty cannot be ameliorated by more or finer measurements but must be recognized and accounted for as best is possible.

Measurement Uncertainty: Uncertainty is introduced when measuring quanties of interest for a variety of reasons. Often we cannot measure the entire population of interest and instead must take samples which introduces sampling variability. Furthermore, there may be detection error when sampling or documentation error when recording measurements. Additionally, there may be error in the measurments themselves.

Parameterization Uncertainty: The extraction of specific probability distributions from data can be challenging. This can arise in predictive models if the exact values of the input parameters are unsure. This can also include model uncertainty if the underlying form of the parameter of interest is mis-specified (e.g. data is assumed to be normally distributed but isn’t).

Description Uncertainty: Finally, the form of the model or even the fundamental science behind certain data might be unknown. The nature and consequences of this uncertainty differ depending on our end goals. For instance, prediction of phenomena may be possible without a accurate mechanistic models but inference and scienfitic understanding will be misled. Because our scientific understanding shapes which data we collect, description uncertainty closes the cycle.

In addition to the data-induced uncertainty, the method-induced uncertainty should be considered.

Contributors

Jordan A. Gault Tamadur Albaraghtheh