Examples of Markov Processes#
Part of a series: Stochastic fundamentals.
Follow reading here
The Wiener Process#
The Wiener process is one of the simplest examples of a Markov process. It has neither jumps, nor drift but only a constant diffusion. In the following, we set the diffusion coefficient \(b=1\) for the sake of simplicity. For historical reasons one calls the random variable \(W_t\).
The Fokker-Planck equation for the random variable \(W_t\) reads
\(\begin{align}
\frac{\partial}{\partial t} p(w, t | w_0, t_0) = \frac{1}{2} \frac{\partial^2}{\partial w^2} p(w,t|w_0,t_0)
\end{align}\)
The FPE can be solved rather easily using the characteristic function
\(\begin{align}
\varphi(s, t) &= \int dw \; p(w,t | w_0, t_0) e^{isw}\\
\Rightarrow \frac{\partial}{\partial t} \varphi &= -\frac{1 }{2} s^2 \varphi
\end{align}\)
For the initial condition
\(\begin{align}
p(w, t_0 | w_0, t_0) &= \delta(w-w_0) \Longleftrightarrow \varphi(s, t_0) = e^{i s w_0}
\end{align}\)
the solution reads
\(\begin{align}
\varphi(s,t) &= \exp{(i s w_0 - \frac{1}{2} s^2(t-t_0))} .
\end{align}\)
Fourier inversion yields
\(\begin{align}
p(w,t|w_0, t_0) &= \frac{1}{\sqrt{2\pi (t-t_0)}} \exp{\left( -\frac{(w-w_0)^2}{2(t-t_0)} \right)}
\end{align}\)
That is, \(W_t\) is a normally distributed random variable with expected value \(w_0\) and a variance taht grows linearly in time as \((t-t_0)\).
Independence of Increments#
The Wiener process is the model for noise in continuous systems and we derive a property which is extremely important for applications - both in Monte Carlo simulations and in the theory of stochastic differential equations.
The joint probability density at time \(t_n \geq t_{n-1} \geq ...\) can be written using the Markov property as
\(\begin{align} &p(w_n t_n; w_{n-1}t_{n-1}; w_{n-1}t_{n-1}; \dots; w_{0}t_0) \\ &=\prod\limits_{i=0}^{i+1} \underbrace{p(w_{i+1}t_{n-1} | w_{i}t_{i})}_{=\frac{1}{\sqrt{2 \pi (t_{i+1}- t_i)}} \exp{\left( - \frac{(w_{i+1}-w_i)^2}{2(t_{i+1} - t_i)}\right)}} \; p(w_{0},t_{0})\\ \end{align}\)
We thus find that the increments \(\Delta W_i = W(t_i) - W(t_{i-1})\) are independent random variables with a Gaussian distributions with \(E(\Delta W_i)=0\) and \(V(\Delta W_i) = \delta t_i=(t_i-t{i-1})\). In any simulation we thus need only independent normal random variables to go from \(t_{i-1}\) to \(t_i\).
The Ornstein- Uhlenbeck process#
The Wiener process does not have a stationary state - the variance growth linearly with time. A deterministic drift term can counteract the ongoing diffusion and lead to a stationary state, which is desirable in many applications.
If we add a linear drift term, we obtain the Ornstein-Uhlenbeck process described by the FPE
\(\begin{align} \frac{\partial}{\partial t} p = \frac{\partial}{\partial x} (k x p) + \frac{1}{2} D \frac{\partial^2}{\partial x^2} \end{align}\)
where \(p\) is a shorthand notation for \(p(x,t|x_0, 0)\). The corresponding equation for the characteristic function
\(\begin{align} \varphi (s,t) &= \int e^{isx} \; p(x,t|x_0, 0) dx \end{align}\)
reads
\(\begin{align} \frac{\partial}{\partial t} \varphi + k s \frac{\partial}{\partial s} \varphi = - \frac{1}{2} D s^2 \varphi \end{align}\)
which is solved by
\(\begin{align} \varphi(s, t) = \exp{\left( \frac{- D s^2}{4 k}(1 - e^{-2kt}+ i s x_0 e^{-kt})\right)} \end{align}.\)
This is a Gaussian distribution with expected value and variance
\(\begin{align} E(X_t) &= x_0 e^{-kt}\\ V(X_t) &= \frac{D}{2 k}\left[ 1 - e^{-2 k t} \right]. \end{align}\)
As time \(t \longrightarrow + \infty\) the distribution relaxes to a stationary state - a Gaussian with \(E(X_t) = 0\) and \(V(X_t)=\frac{D}{2k}\). We can obtain the solution in a simpler way by setting \(\partial p / \partial t = 0\) which yields
\(\begin{align} \frac{\partial}{\partial x} \left[ k x p + \frac{1}{2} D \frac{\partial}{\partial x} p \right] = 0 \end{align}\)
Integrating once gives
\(\begin{align} \left[ k x p + \frac{1}{2} D \frac{\partial}{\partial x} p \right]_{-\infty}^{x} = 0 \end{align}\)
Normalisation requires \(p(-\infty) = \partial p / \partial x |_{-\infty}=0\) such that
\(\begin{align} \frac{1}{p} \; \frac{\partial p}{\partial x} &= - \frac{2 k x}{D}\\ \Leftrightarrow \log(p) &= -\frac{2 k x}{D} + \text{constant}\\ \Rightarrow p(x) &\propto \exp{\left( - \frac{kx^2}{D}\right)} \end{align}\)
The stationarity refers to the distribution (more precisely the conditional PDF \(p\)) - it does not mean that the random variable \(X_t\) assumes a constant value! Let us illustrate this residual stochasticity in terms of the autocorrelation \(\langle X_t \ X_{t'}\rangle_s\) where the subscript \(s\) refers to the stationary state.
The autocorrelation indicates how strongly the process is correlated at the two times \(t\) and \(t'\).
We have (assuming \(t>t'\) w.l.o.g)
\(\begin{align} &\bigg\langle X_t X_{t'} \;| \; [x_0, t_0] \bigg\rangle \\ &= \int \int dx_1 \; dx_2 \; x_1 \; x_2 \; p(x_1 t, x_2 t' | x_0 t_0)\\ \text{Markov} \longrightarrow &= \int \int dx_1 \; dx_2 \; x_1 \; x_2 \; p(x_1 t | x_2 t') \; p(x_2 t' |x_0 t_0) \end{align}\)
We approach the stationary distribution by letting \(t_0 \Longrightarrow -\infty\) such that
\(\begin{align} p(x_2 t' | x_0 t_0) \longrightarrow \sqrt{\frac{k}{\pi D}} \exp{\left( -\frac{k x^2}{D}\right)} \end{align}\)
But for \(p(x_1 t | x_2 t')\) we must include the full conditional probability density which yields
\(\begin{align} \int dx_1 \; x_1 \; p(x_1 t | x_2 t') &= x_2 e^{-k(t-t')}\\ \langle X_t X_{t'}\rangle_s &= \int dx_2 x_2^2 e^{-k(t-t')} \sqrt{\frac{k}{\pi D}} \exp{\left( - \frac{k x_2^2}{D}\right)}\\ &= \frac{D}{2k} e^{-k(t-t')} \end{align}\)
That is, the autocorrelation decays exponentially with the time difference \(t-t'\)! If we probe the position \(X_t\) at a short time difference, the positions will still be very close. If we probe the position again after a long time difference, the correlation have decayed to almost zero and the outcome is described by the stationary distribution. More generally, The autocorrelation function of a stationary process depends only on the difference \(t-t'\).
Poisson Process#
Let us consider a simple model of a growth process. Individuals are born at a constant rate \(\lambda\):
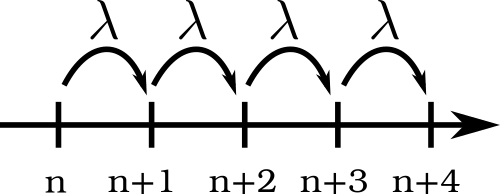
Fig. 13 Simple model of a growth process.#
The discrete stochastic process is described by a Master equation with
\(\begin{align} w(n+1 | n, t) &= \lambda\\ w(n, m t) &= 0 \quad \text{else}.\\ \longrightarrow \frac{\partial}{\partial t} P(n,t | n', t') &= \lambda \left[ P(n-1, t | n', t') - P(n,t|n',t') \right] \end{align}.\)
The characteristic function
\(\begin{align} \varphi(s,t) = E(e^{ins}) = \sum\limits_n P(n,t | n', t') e^{ins} \end{align}\)
then satisfies
\(\begin{align} \frac{\partial}{\partial t} \varphi(s, t) &= \lambda \sum\limits_n P(n-1, t | n', t') e^{ins} - P(n,t|n',t') e^{ins}\\ &= \lambda \left( e^{is} - 1 \right) \varphi(s, t)\\ \Rightarrow \varphi(s,t) &= \exp{\left[ \lambda t (e^{is}-1)\right]} \end{align}\)
We get back the probability mass function by Fourier decomposition. Assuming that the system is empty at \(t=0\) we have
\(\begin{align} P(n,t|0,0) &= \frac{e^{-\lambda t} (\lambda t)^2}{n!} \end{align}\)
i.e. a Poisson distribution with expected value
\(\begin{align} E(N_t) &= \lambda t \end{align}\)
Random Telegraph Process#
The word telegraph refers to a process that can assume only two states: on or off.
So consider a stochastic process with only two states \(a\) and \(b\). Hopping between the two states happen with rates \(\lambda\) and \(\mu\):
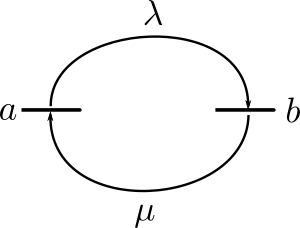
Fig. 14 Random Telegraph Process.#
The master equation for this process reads:
\(\begin{align} \frac{\partial}{\partial t} P(a t | x t_0) = - \lambda P(a t|x t_0) + \mu P(b t|x t_0)\\ \frac{\partial}{\partial t} P(b t | x t_0) = + \lambda P(a t|x t_0) - \mu P(b t|x t_0) \end{align}\)
We first consider the stationary state, that is found by setting \(\frac{\partial P}{\partial t} = 0\), with the result
\(\begin{align} \lambda P(at|xt_0) - \mu P(bt|xt_0) &= 0\\ \Rightarrow \frac{P(a t | x t_0)}{P(b t | x t_0)} &= \frac{\mu}{\lambda}. \end{align}\)
Together with the normalization condition \(P(a t | x t_0)+P(b t | x t_0)=1\) we thus find
\(\begin{align} P_{s}(a t | x t_0) = \frac{\mu}{\mu + \lambda}, \quad \quad P_s(b t | x t_0) = \frac{\lambda}{\mu + \lambda} \end{align}\)
with the expected value and the variance
\(\begin{align} E_s(X_t) &= \frac{a \mu + b \lambda}{\mu + \lambda}\\ V_s(X_t) &= \frac{(a-b)^2 \mu \lambda}{(\lambda + \mu)^2} \end{align}\)
The time dependence of the process is captured by the evolution of the conditional probability density functions. One can show that
\(\begin{align} P(a t|x t_0) &= \frac{\mu}{\lambda + \mu} + e^{-(\lambda + \mu)(t-t_0)} \left( \frac{\lambda}{\mu + \lambda} \delta_{ax}- \frac{\mu}{\mu + \lambda} \delta_{bx} \right)\\ P(b t|x t_0) &= \frac{\lambda}{\lambda + \mu} + e^{-(\lambda + \mu)(t-t_0)} \left( \frac{\lambda}{\mu + \lambda} \delta_{ax} - \frac{\mu}{\mu + \lambda} \delta_{bx} \right) . \end{align}\)
As for the OU-process we can use these results to compute the autocorrelation in the stationary state (\(t>t'\) w.l.o.g)
\(\begin{align} \langle X_t X_{t'} \rangle_s &= \sum\limits_{x,x'} x x' P(xt|x's) P_s(x') \end{align}\)
After a little algebra one finds that
\(\begin{align} \langle X_t X_{t'}\rangle_s &= \frac{(a-b)^2 \mu \lambda}{(\lambda + \mu)^2} \; e^{-(\lambda + \mu) |t-t'|} . \end{align}\)
That is, the autocorrelation decay exponentially similar to the OU-process.
