Sensitvity Analysis [DRAFT]#
This article is part of a series: Sensitivity analysis. The following aspects are covered
Problem set-up and methods:
Use Cases
Sensitivity analysis is an important tool in uncertainty quantification that helps to understand the effects of uncertainties and variations in the inputs of a model on the output or response of the model. In other words, sensitivity analysis is used to determine which input parameters and/or boundary conditions have the most significant impact on the output or response of a model. Moreover, it is used to test the robustness of the model under given uncertainties. It is used in the fields from applied mathematics, engineering, finance, environmental science, and others, where the behavior of a system is dependent on several input parameters. It is an essential tool as it provides insights into which input parameters should be focused on when reducing uncertainties or improving the model’s accuracy. It used to identify critical input parameters and their interactions, which can be used to optimize the model design or to make informed decisions under uncertainties. There are many different techniques for performing sensitivity analysis and this article is a short overview of the methods used for sensitivity analysis.
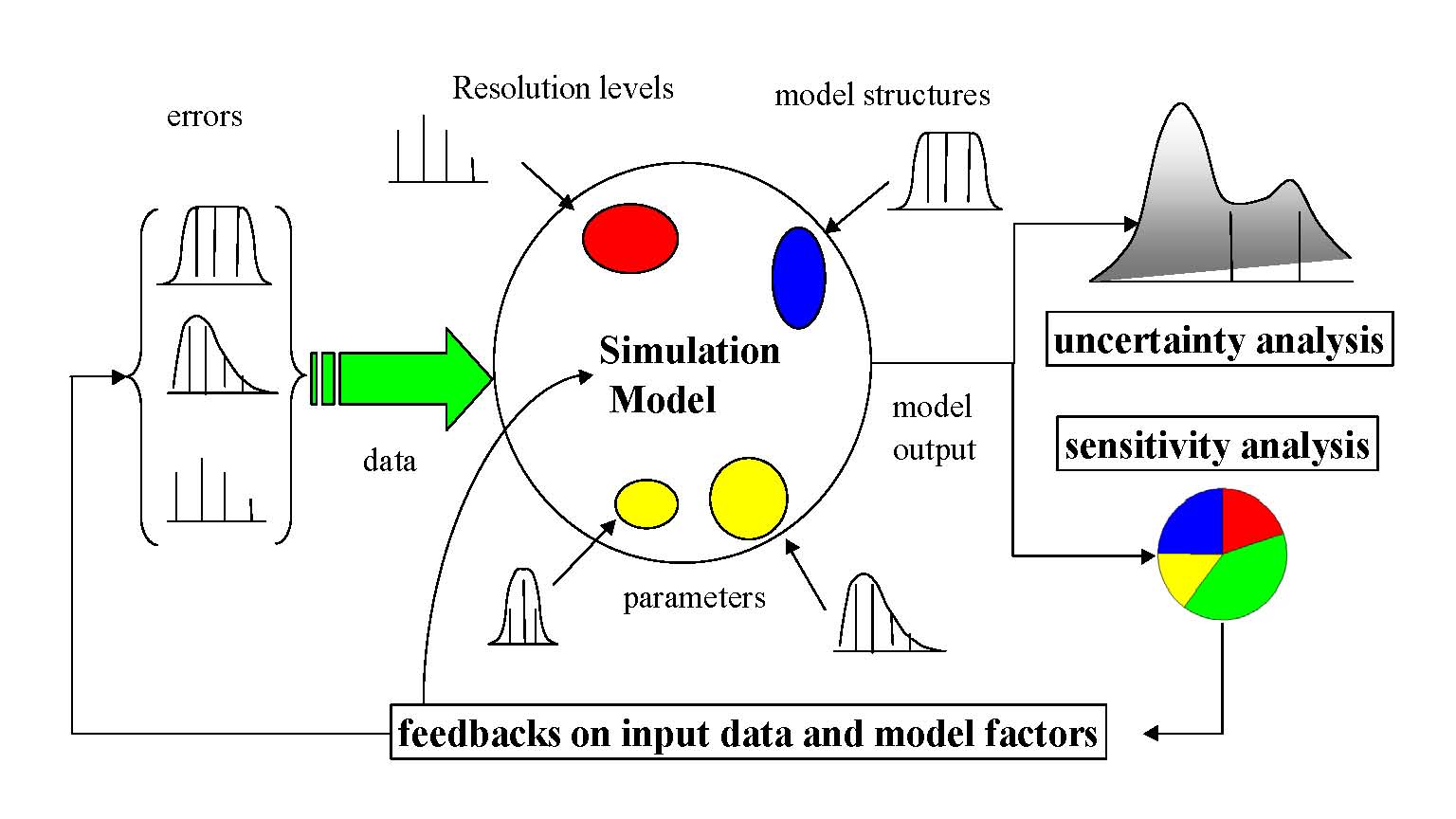
Sensitivities studies can be divided into two categories namely, local sensitivity analysis and global sensitivity analysis. Local sensitivities can be defined as derivatives of a model with respect to the parameters at a single point in the uncertain parameter space. However, global sensitivities bring up an idea of probabilistic programming, i.e. how does the output changes generally with respect to the input over the whole uncertain input space. Indeed, there aren’t exact definitions of local and global sensitivity analysis.
It is important here to clarify two important terms namely, model and parameters. In this article while refereeing to the term a ‘model’, it can be used for a Neural Network (NN), a mathematical approximation of a physical process for example a model defined by ordinary differential equations or partial differential equations or it could be a regression model based upon data. On the other hand the term ‘parameters’ can be used for the model input. For example, it could be initial conditions and boundary values in ODEs and PDE, or it could be inputs of NN. In some fields like climate and ocean modelling, ‘parameters’ could mean temperature, pressure, a wind drag coefficient influencing the effect of the atmosphere and ocean surface and etc.
In order to state the problem which sensitivity analysis undertakes, let’s consider a model
Recall, that the model \(f\) can be a NN or an ODE problem and \(x_i\) can be input parameters as discussed above. The goal is to understand and quantify the change in \(y\) with respect to the change in \(x_i\). However, in order to perform the sensitivity studies we need a domain and the distribution of \(x_i\) which makes \(x_i\) a random variable. Thus, we have a deterministic program \(f\) with probabilistic inputs and we want to determine the effects of the given probabilistic inputs on the distribution of output.
In conclusion, sensitivity analysis plays a crucial role in uncertainty quantification across various fields, including applied mathematics, engineering, finance, and environmental science. By examining the impact of input variations on model outputs, sensitivity analysis provides valuable insights for optimizing model designs, reducing uncertainties, and making informed decisions. This article has provided a comprehensive overview of different sensitivity analysis methods, emphasizing their significance in understanding the behavior of models under uncertainties and the importance of identifying critical input parameters for improved accuracy.
Contributors#
Tamadur Albaraghtheh
