Optimization of Financial Risk Measures

Part of a series: Optimization Under Uncertainty.

Follow reading here

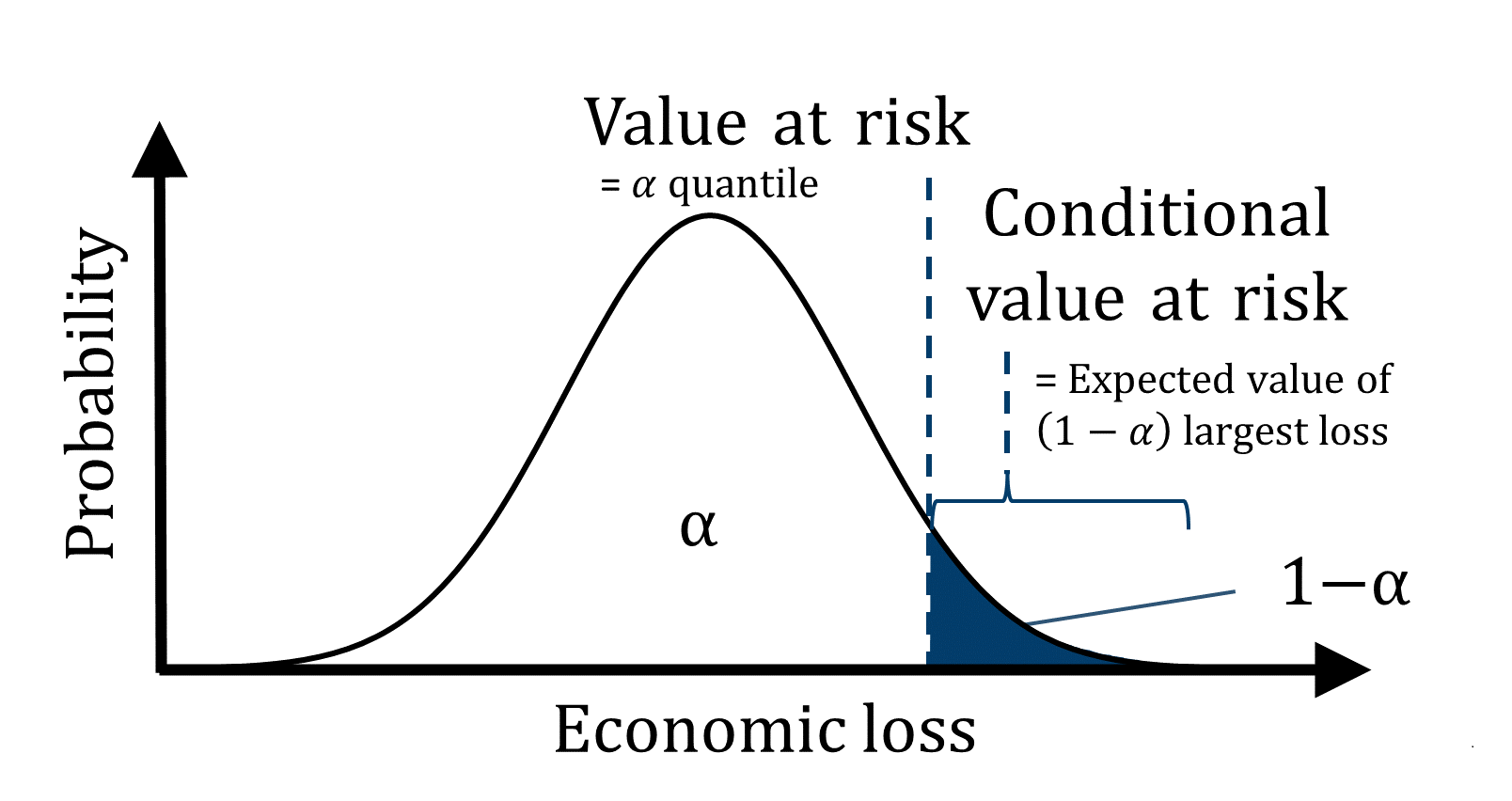
For any investment project, the expected cost (c.f. stochastic programming) is a decisive measure. In addition, it is advisable to consider and optimize the associated financial risks, i.e., cost associated to worst case scenarios. If the economic outcome is uncertain, one can use various measures to quantify the associated financial risk and choose an appropriate investment strategy. Two popular measures frequently used in stochastic programming are the \(\alpha\)-Value at Risk and the Conditional Value at Risk (Figure 1).

The \(\alpha\)-Value at Risk refers to the \(\alpha\) quantile and can formally be described with the following equation [Rockafellar and Uryasev, 2000].

\[ \begin{equation} \begin{aligned} VaR (\alpha) = \underset{t}{\text{min }} t \text{ s.t. } P(x \leq t) \geq \alpha \end{aligned} \end{equation} \]

With \(P\) referring to the distribution function of the economic loss, e.g., uncertain cost associated to investments, \(P(x \leq t)\) is the probability that the uncertain economic loss \(x\) is less than or equal to a threshold \(t\). The Value at Risk corresponds to the minimized threshold, which meets the condition that \(P(x \leq t)\) is greater than \(\alpha\). The uncertain loss \(x\) will be smaller than the resulting \(\alpha\)-Value at Risk with a probability \(\alpha\), where \(\alpha\) is a choosen confidence level. For example, if the 95%-Value at Risk is 1 mio Euro, then in 95% of the cases the economic loss will be below 1 mio Euro and in 5% of the cases the economic loss will be above 1 mio Euro.

Figure 1: The Value at Risk refers to the \(\alpha\) quantile. The expected cost of the \((1-\alpha)\) quantile with the most economic loss is the Conditional Value at Risk.

While the \(\alpha\)-Value at Risk can be understood as the best of the \((1-\alpha)\)-probable worst outcomes, the Conditional Value at Risk characterizes these risky, worst cases by their expected value, which is important for distributions with long tails. The Conditional Value at Risk [Rockafellar and Uryasev, 2000] is defined as the expected value of the economic loss that is greater than the Value at Risk:

\[ \begin{equation} \begin{aligned} CVaR (\alpha) = E[x|x \geq VaR(\alpha)] \end{aligned} \end{equation} \]

For example, if the 95%-Conditional Value at Risk is 1 mio Euro, then the expected cost of the economic loss for the 5% worst case scenarios is at 1 mio Euro.

Note

\(\bullet\) The Value at Risk does not fullfill the property of subadditivity, i.e., the Value at Risk of the sum of two random variables is smaller or equal to the sum of the Value at Risk of each individual random variable. In contrast, the Conditional Value at Risk has this useful property and is therefore a so-called coherent risk measure and more commonly used in practice [Artzner et al., 1999].

\(\bullet\) Risk measures can be integrated into optimization problems with uncertain variables, i.e., stochastic programs. One can set constraints on the risk measures in stochastic programs, consider them as part of the objective function, or use bi-objective optimization to make optimal investment decisions while restricting the associated risks.

References

ADEH99

Philippe Artzner, Freddy Delbaen, Jean-Marc Eber, and David Heath. Coherent Measures of Risk. Mathematical Finance, 9(3):203–228, jul 1999. URL: http://doi.wiley.com/10.1111/1467-9965.00068, doi:10.1111/1467-9965.00068.

RU00(1,2)

R. Tyrrell Rockafellar and Stanislav Uryasev. Optimization of conditional value-at-risk. The Journal of Risk, 2(3):21–41, 2000. doi:10.21314/jor.2000.038.

Author

Sonja Germscheid

Contributors

Manuel Dahmen