Uncertainty Sources In Degradation Models#
Part of a series: Uncertainty quantification in Implants Materials.
Follow reading here
Surrogate modelling approach in Implants Materialsin under uncertainty
The main sources of uncertainties, which directly affect the estimation of the degradation rate in material science can be summarized as: Environmental factors, the degradation rates of metal can be affected by environmental factors such as temperature, humidity and the presence of corrosive agents such as salts, acids, gases and cells. There is uncertainty regarding the information related to these factors, and variations within these factors can result in fluctuations in degradation rate measurements and overall predictions of degradation behavior. Furthermore, Material variability, in which the composition and structure of the metal can impact its degradation resistance. Variations in the microstructure or chemical composition of the metal can lead to different degradation rates. Another source affecting the degradation rates is Surface conditions. The presence of surface roughness, defects, or other contaminants can also affect the degradation rate. In addition, surface treatments such as coatings or treatments can also impact the degradation resistance of the metal [Kersaudy et al., 2015, Zhang et al., 2020]. Moreover, the Testing methodology used to test the degradation rate of a metal can introduce uncertainty. Different testing techniques used for the analysis with different accuracies can provide varying results. Moreover, both Degradation models and Numerical errors are directly affecting the accuracy of predicting the degradation rate. The accuracy of degradation models, which are used to predict the degradation rate of metals, can be limited by a lack of data or limited understanding of the underlying degradation mechanisms [Albaraghtheh et al., 2022, Kersaudy et al., 2015]. The discretization techniques, moreover, are also important sources for introducing and propagating the uncertainty with the degradation models [Albaraghtheh et al., 2022]. To create a reliable mathematical framework that can accurately simulate the degradation process of Mg-based implants, it is highly important to quantify the various uncertainties associated with different aspects of the degradation process [Albaraghtheh et al., 2022].
Models simulating the degradation of Mg-based implants are complex and expensive to evaluate due to the multi-scale and multidimensional nature of the degradation process. Different sources of uncertainty are associated with the degradation process, which are illustrated in Fig. 80. These sources within the degradation process of Mg-based implants propagate from the uncertainties in the experimental measurements to the uncertainties introduced by the experimental data to the calibration process, which will affect the parameters of the model and potentially result in errors in the modelling process. Even though a mathematical model is uncertain by itself, it can still be accurate as long as the assumptions used to build it are true [Albaraghtheh et al., 2022, Kersaudy et al., 2015]. Predictions based on computational models are subject to discretization errors [Kersaudy et al., 2015]. Through the sub-models that are used to evaluate the model parameters, transport properties, constitutive relations, equations of state and source term rate parameters, various uncertainties build up [Kersaudy et al., 2015, Zhang et al., 2020]. The different uncertainties within the submodel will propagate within the model, affecting its predictions. Model-based decisions will be affected by the accumulated uncertainty within the system [Böttcher et al., 2021, Ghanem et al., 2017, Sobester et al., 2008].
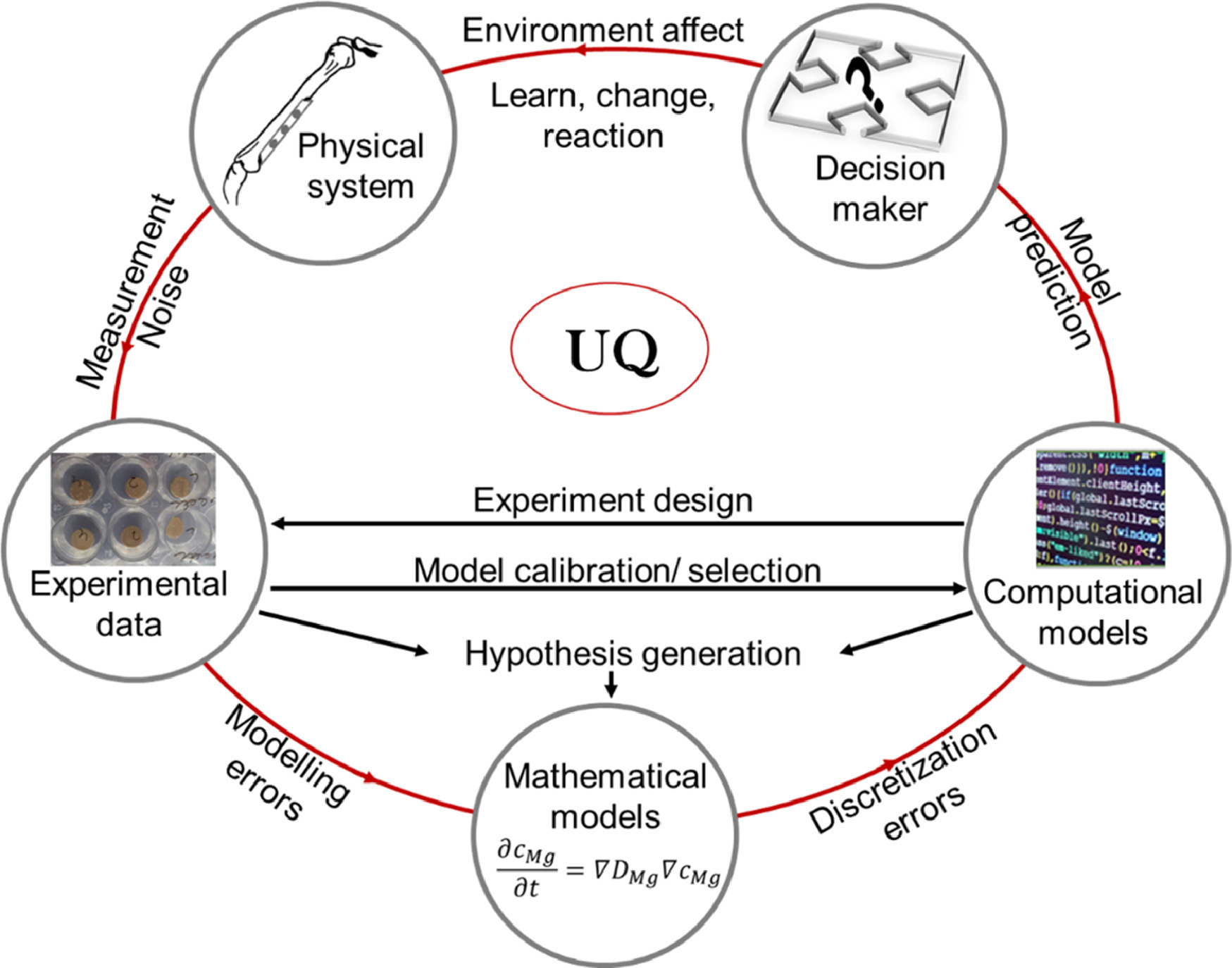
Fig. 80 Schematic diagram of uncertainty sources within the degradation process of Mg-based implants, the red arrows represents the building of uncertainty within the system. (adapted under CC-BY-4.0 license [Albaraghtheh et al., 2022]).#
Several approaches are found in literature to quantify these uncertainties within the different systems. In the current project, we consider the implementation of surrogate models to calibrate and perform further non-intrusive uncertainty quantification analysis. The utilization of surrogate models has been shown to efficiently reduce computational costs and time, particularly in situations where simulations are expensive or when a lack of conceptual understanding exists between input and output variables [Albaraghtheh et al., 2022, Alizadeh et al., 2020]. In the current case study, we are using Kriging, Polynomial Chaos Expansion and Polynomial Chaos Kriging surrogate models to calibrate the key parameters of the degradation models, e.g. reaction rate constants, diffusion parameters and porosity. Furthermore, this approach reduces the computational cost and enable further UQ analysis such as sensitivity analysis, reliability studies and quantifying the propagation of uncertainty associated the degradation models.
References#
- AWRomerZP22(1,2,3,4,5,6)
Tamadur Albaraghtheh, Regine Willumeit-Römer, and Berit Zeller-Plumhoff. In silico studies of magnesium-based implants: a review of the current stage and challenges. Journal of Magnesium and Alloys, 2022.
- AAM20
Reza Alizadeh, Janet K Allen, and Farrokh Mistree. Managing computational complexity using surrogate models: a critical review. Research in Engineering Design, 31:275–298, 2020.
- BottcherLF+21
Maria Böttcher, Ferenc Leichsenring, Alexander Fuchs, Wolfgang Graf, and Michael Kaliske. Efficient utilization of surrogate models for uncertainty quantification. PAMM, 20(1):e202000210, 2021.
- GHO+17
Roger Ghanem, David Higdon, Houman Owhadi, and others. Handbook of uncertainty quantification. Volume 6. Springer, 2017.
- KSV+15(1,2,3,4,5)
Pierric Kersaudy, Bruno Sudret, Nadège Varsier, Odile Picon, and Joe Wiart. A new surrogate modeling technique combining kriging and polynomial chaos expansions–application to uncertainty analysis in computational dosimetry. Journal of Computational Physics, 286:103–117, 2015.
- SFK08
András Sobester, Alexander Forrester, and Andy Keane. Engineering design via surrogate modelling: a practical guide. John Wiley & Sons, 2008.
- ZYW20(1,2)
Juan Zhang, Junping Yin, and Ruili Wang. Basic framework and main methods of uncertainty quantification. Mathematical Problems in Engineering, 2020:1–18, 2020.
Contributors#
Houda Yaqine, Berit Zeller-Plumhoff
