Model Parameterization in Transdimensional Scheme (Draft)

Introduction

In a transdimensional scheme, the parametrization of the model and dimension is allowed to change or jump between different model parametrizations and dimensions. It not only provides sufficient flexibility to explore various model space (different parameter combination) but also lets data itself has the chance to dictate the model complexity resulting in a parsimonious result.

More details about how to introduce trans-dimensional problems from the Bayesian scheme can be found in Transdimensional Markov chain Monte Carlo . Reversible Jump Markov chain Monte Carlo (RJ-MCMC) sampling algorithm which allows probabilistic sampling in variable dimension spaces is usually used in transdimensional Bayesian inference. With the introduction of the birth and death proposal steps, these sampling schemes are able to make trans-dimensional steps between different model parametrizations.

Voronoi Cells

Voronoi cells (Fig. 43) built from a set of nuclei are the most used parametrization method in transdimensional problems. In the Voronoi cell parameterization, the model is defined using a number of nuclei (nodes) in a bounded plane (1D, 2D) or volume (3D) to represent the Voronoi cell centers. For each nucleus (node), there will be a corresponding region consisting of all points closer to that nuclei than to any other nuclei. These regions are called Voronoi cells. Each Voronoi nuclei can be assigned to a set of one or more model parameters and the corresponding Voronoi cell also has the same parameters as nuclei. It means that this parameterization produces surfaces with constant values (based on values of nuclei) in each Voronoi cell and discontinuities at Voronoi cell edges.

In transdimensional problems, these Voronoi cell parametrizations can be locally adapted by iteratively adding (‘birth’) and removing (‘death’) a single nuclei point and its associated parameter values by perturbing the Voronoi cell. Through data-driven addition or deletion of Voronoi nodes, As the algorithm proceeds, a number of models with different dimensions are sampled and allow to fit the observations in different degrees.

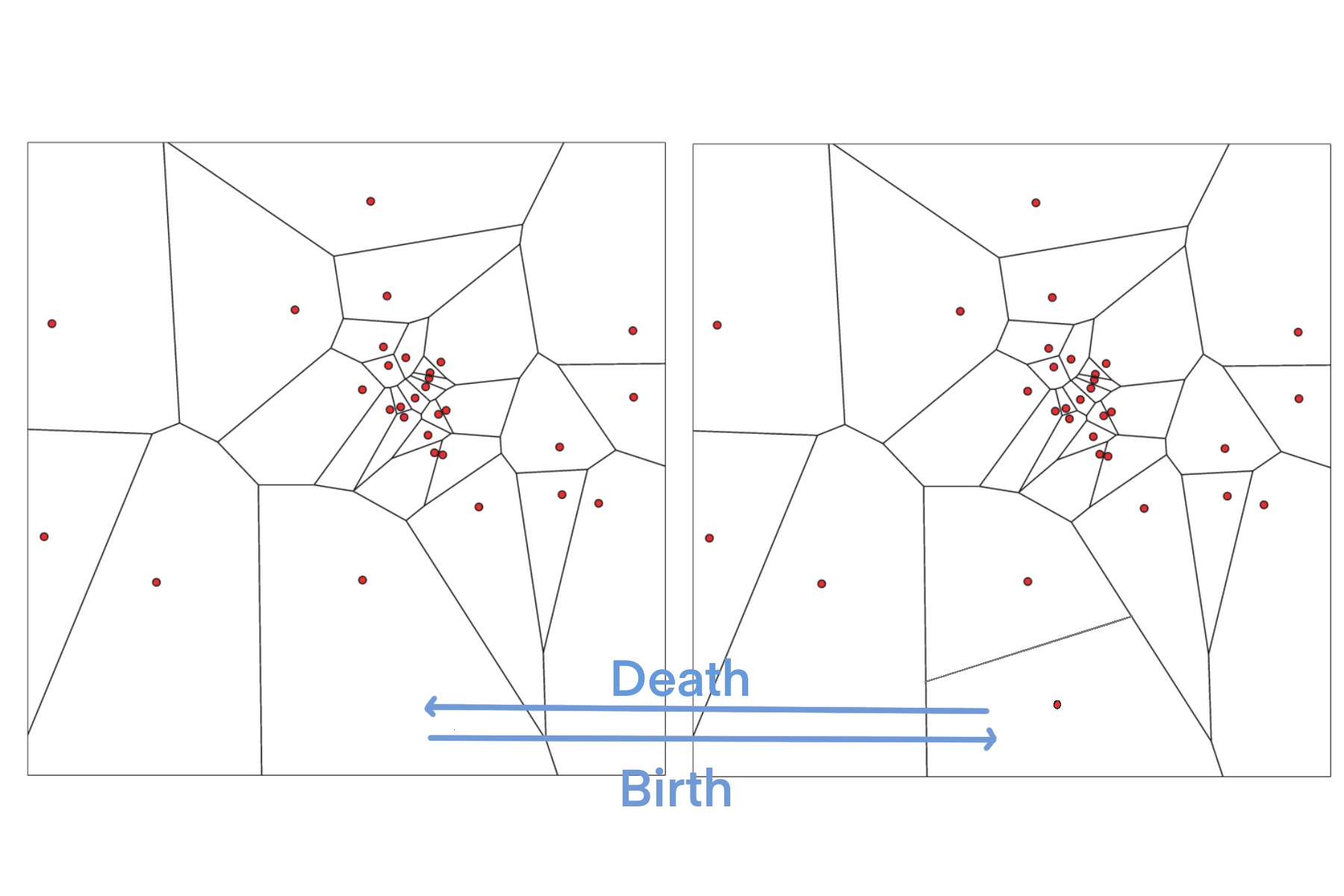
Fig. 43 Illustrations show birth (from a to b) and death (from b to a) steps in Voronoi cells parametrizations. Figure is modified from [Bodin et al., 2012].

Tree-Based

Trans-dimensional sampling over tree structures uses an abstract tree to subdivide any space. It employs a model parameterization with a hierarchy or multiresolution analyses that range from coarse to fine-scale. Fig. 44 can explain this hierarchy concept by introducing a tree structure of quaternary trees. Level 1 (top level) corresponding to the root node of the tree with a single pixel representation of an average value of a field of a 2-D domain is subdivided into four subpixels at the next level and so on. We can see that Level 2 has four children nodes spaned from the root.The tree depth is constrained by the size of the forward model grid. Each successive depth level represents scaled features from corse to fine in the model parematerization.

Here, each child node can be added one or more nodes to a tree at a finer spatial resolution or removed at a coarser level through successive levels of local perturbation terms. Compared to Voronoi cells, this tree-based approach builds models in a top to down, coarse to fine scale construction. It enables efficient forward model processing if forward computation based on grids resolution as coarse scale takes lower computation cost. Furthermore, it produce a continuous field which Voronoi cells don’t present well.

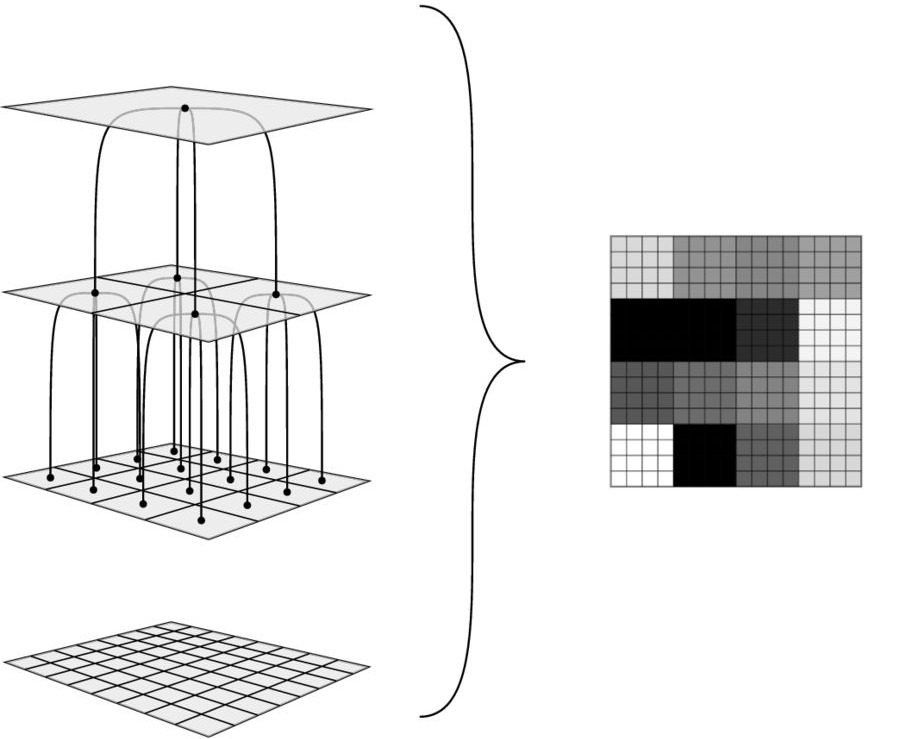
Fig. 44 A hierarchy tree structure from the coarse to the fine scale. The tree span from a single root node of the tree and are subdivided into four children nodes at the next level and so on. Figure is modified from [Hawkins and Sambridge, 2015].

References

BSRA12

Thomas Bodin, Malcolm Sambridge, Nick Rawlinson, and Pierre Arroucau. Transdimensional tomography with unknown data noise. Geophysical Journal International, 189(3):1536–1556, 2012.

HS15

Rhys Hawkins and Malcolm Sambridge. Geophysical imaging using trans-dimensional trees. Geophysical Journal International, 203(2):972–1000, 2015.

Author

Kuan-Yu Ke

Contributors

Maqsood Rajput, Tamadur Albaraghtheh, Houda Yaqine