Surrogate Modelling Approach#
Part of a series: Uncertainty quantification in Implants Materials.
Follow reading here
Surrogate Models#
It is necessary to repeatedly evaluate computational models when uncertainty is quantified or optimization is taken into account. This task cannot be accomplished by costly mathematical models. A surrogate model is constructed and evaluated instead of the original model to alleviate the computational burden. The surrogate models can be viewed as functional approximations that are built based on the original computational models; these models are more compact and faster to evaluate in a domain of interest defined by input parameters [Sobester et al., 2008, Wang et al., 2021, Kersaudy et al., 2015, Zhang et al., 2020]. Surrogate models are frequently used in data-driven appraches, in which data is utilized to reflect the behavior of a physical system. The need for such tool in these applications because the need for interpolation of the data from the deterministic simulations, e.g. finite element method (FEM) and finite volume methods (FVM). The main challenge most of those practical design problems share is that a single FEM simulation can take numerous hours or even days. The well-trained surrogate model will replace the original computational model for further UQ and sensitivity analysis, in which a large number of model evaluation is needed [Sudret et al., 2017].
The choice of a surrogate model depends on the complexity of the system being modeled and the desired accuracy of the model. The more complex the system, the more complex the model will need to be in order to accurately approximate the behavior of the system. Additionally, the accuracy of the model will depend on the amount of data available and the accuracy of the data points. Finally, the type of model chosen will depend on the type of data available, such as whether the data points are linear or non-linear [Böttcher et al., 2021, Ghanem et al., 2017, Sobester et al., 2008, Sudret et al., 2017]. Surrogate models can be categorized according to their types, the data needed for their construction, or training strategies. Additionally, these models can be further classified based on their specific applications. In recent times, there has been a development of hybrid surrogate models, wherein multiple surrogate models are combined together [Böttcher et al., 2021, Ghanem et al., 2017, Sobester et al., 2008, Hou and Behdinan, 2022].
Constructing Surrogate Models#
In non-intrusive UQ approach, the computationally expensive model is treated as a black-box. The training data for the surrogate model are sampled from the input distribution in the parametric space of the input parameters. The sampled parameter combinations are evaluated using the expensive computational model (black-box) and the resulting observations are exploited to build the surrogate model on the whole domain of the input distribution [Al Baraghtheh et al., 2023]. Figure Fig. 35. Note that, the sampling of the input variable range should be representative and capture all possible information about the original computational model [Wang et al., 2016].
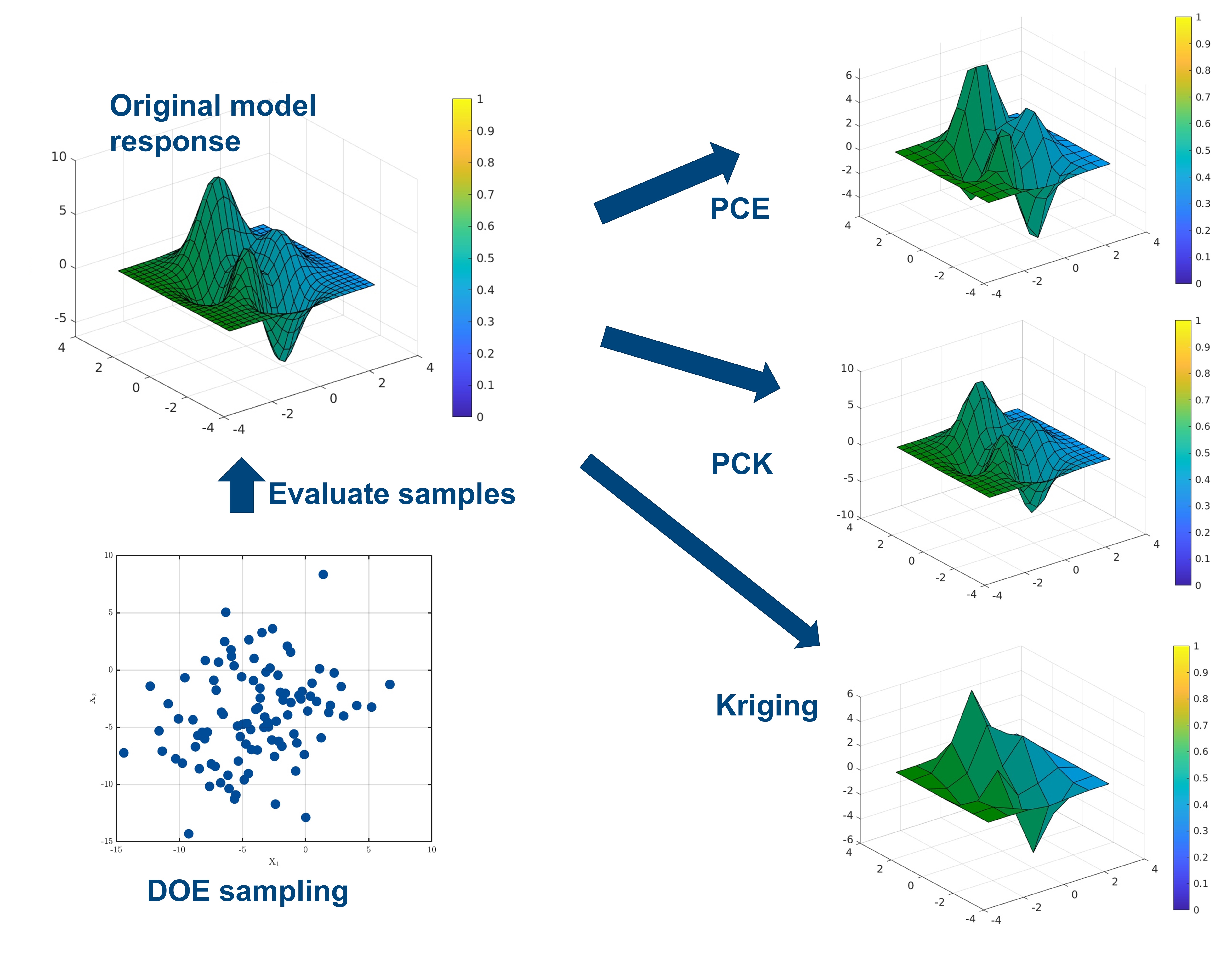
Fig. 35 Schematic diagram of the construction of surrogate models for degradation model. (Inspired by [Dong et al., 2019]).#
The training data, also known as numerical experiment design (DOE), is generated by evaluating the balck-box model output for a certain number of generated sample points of the input parameter vector. Here, the black-box form can be a physical or computer experiment; e.g. finite element code. The quantity of interest (QoI) simulated by the surrogate model, which for the degradation models could be volume loss, degradation rate or mass loss. The general mathematical presentation of the surrogate model is
where \(\mathcal{M}\) is the surrogate shape function that maps the black-box model for the input parameters \(f(\textbf{x})\), which is presented as a vector \(\mathcal{M}(\textbf{x})\) in \(\subset\mathbb{R}^M\), to a vector of QoI, which is denoted by \(\textbf{y}\). The accuracy and reliability of surrogate models must be validated. Validation of the surrogate model predictions against the original complex model or experimental data [Sudret et al., 2017, Zeller-Plumhoff et al., 2022]. Therefore, it is essential to establish appropriate validation procedures and metrics to assess the performance of the surrogate models, for example using leave-out-error \(\varepsilon_{LOO}\) to estimate the performance of surrogate models, which is given by [Zeller-Plumhoff et al., 2022]
Surrogate Models In Application#
In the current case study of quantifying the uncertainty associated the degradation models of biodegradable implants, three different surrogate models are used; Kriging, Polynomial Chaos Expansion and Polynomial Chaos Kriging.
References#
- ABHS+23
Tamadur Al Baraghtheh, Alexander Hermann, Arman Shojaei, Regine Willumeit-Römer, Christian J Cyron, and Berit Zeller-Plumhoff. Utilizing computational modelling to bridge the gap between in vivo and in vitro degradation rates for mg-xgd implants. Corrosion and Materials Degradation, 4(2):274–283, 2023.
- BottcherLF+21(1,2)
Maria Böttcher, Ferenc Leichsenring, Alexander Fuchs, Wolfgang Graf, and Michael Kaliske. Efficient utilization of surrogate models for uncertainty quantification. PAMM, 20(1):e202000210, 2021.
- DSSW19
Huachao Dong, Siqing Sun, Baowei Song, and Peng Wang. Multi-surrogate-based global optimization using a score-based infill criterion. Structural and Multidisciplinary Optimization, 59:485–506, 2019.
- GHO+17(1,2)
Roger Ghanem, David Higdon, Houman Owhadi, and others. Handbook of uncertainty quantification. Volume 6. Springer, 2017.
- HB22
Chun Kit Jeffery Hou and Kamran Behdinan. Dimensionality reduction in surrogate modeling: a review of combined methods. Data Science and Engineering, 7(4):402–427, 2022.
- KSV+15
Pierric Kersaudy, Bruno Sudret, Nadège Varsier, Odile Picon, and Joe Wiart. A new surrogate modeling technique combining kriging and polynomial chaos expansions–application to uncertainty analysis in computational dosimetry. Journal of Computational Physics, 286:103–117, 2015.
- SFK08(1,2,3)
András Sobester, Alexander Forrester, and Andy Keane. Engineering design via surrogate modelling: a practical guide. John Wiley & Sons, 2008.
- SMW17(1,2,3)
Bruno Sudret, Stefano Marelli, and Joe Wiart. Surrogate models for uncertainty quantification: an overview. In 2017 11th European conference on antennas and propagation (EUCAP), 793–797. IEEE, 2017.
- WDT+16
Chen Wang, Qingyun Duan, Charles H Tong, Zhenhua Di, and Wei Gong. A gui platform for uncertainty quantification of complex dynamical models. Environmental Modelling & Software, 76:1–12, 2016.
- WWYC21
Kaiwen Wang, Yinan Wang, Xiaowei Yue, and Wenjun Cai. Multiphysics modeling and uncertainty quantification of tribocorrosion in aluminum alloys. Corrosion Science, 178:109095, 2021.
- ZPAHocheWRomer22(1,2)
Berit Zeller-Plumhoff, Tamadur AlBaraghtheh, Daniel Höche, and Regine Willumeit-Römer. Computational modelling of magnesium degradation in simulated body fluid under physiological conditions. Journal of magnesium and alloys, 10(4):965–978, 2022.
- ZYW20
Juan Zhang, Junping Yin, and Ruili Wang. Basic framework and main methods of uncertainty quantification. Mathematical Problems in Engineering, 2020:1–18, 2020.
Contributors#
Jordan Gault, Berit Zeller-Plumhoff
